A Tool for Generating Perspective Grids 2

5th November 2004

I need a perspective grid for the drawing I’m working on, and I feel that it should be a relatively easy thing to get a computer to produce from some basic information.

"The Beast" (part of the Microcosm project)
This drawing actually uses a ‘curved space’ perspective grid, but a straight-line mathematical perspective grid construction would still be useful for this drawing.

To be able to set up a perspective grid of squares, I should only need:

1. distance between vanishing points,

2. angle beta (from reference grid to left vanishing point),

3. angle alpha (from reference grid to right vanishing point),

4. and then one angle x (for one row of the grid)

The rest should be able to be calculated from these specifications. Eg. the vanishing point for the diagonals should be able to be calculated from these. The computer could calculate the lines with great accuracy, removing the need for long rulers to wide vanishing points. Such a tool for calculating perspective grids would be useful for many future drawings as well. I like the idea of creating such tools.

Maybe, it would be more useful to start with different variables, based on distance measurements that could be more easily made from the drawing I want to produce the grid for.
eg.:

1. distance of reference point to horizon

2. angle to right vanishing point

3. angle to left vanishing point

4. distance of one grid along line to left vanishing point.

What results then did I want to get back? How would the grid be drawn on my drawing. The dimensions along the paper edge might be necessary as well.

1. position of diagonal vanishing point

2. measurements along line to right vanishing point (which might get cut because the paper runs out before getting to the right vanishing point)

3. measurements along line to left vanishing point (which might get cut because the paper runs out before getting to the left vanishing point)

4. From these, I can think of a number of other variables I might need to add to the start of my calculations:

5. number of grids along line to right vp

6. number of grids along line to left vp

7. width of paper (or at least width between vertical reference lines used as virtual paper edges)

8. distance of reference point from left edge of paper (left vertical virtual paper edge reference line)

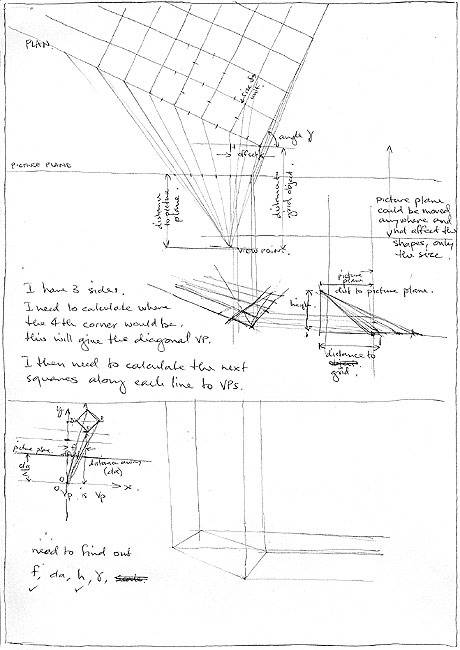
For simplicity, it would be best to use the horizon as the main reference line. This should work well, and be useful for many future drawings.

Unfortunately, I found the mathematics tricky to develop. I could work out the positions of the Vanishing Points easily enough, but I couldn’t see an easy way to determine the grid measurements along each each line to the vanishing points. It also seemed to be vitally important to know where the vanishing point for the diagonals was located along the horizon, but calculating this seemed very complex.

In October 2005, I started looking again at producing the mathematics for generating perspective grids from minimal measurements from a drawing:

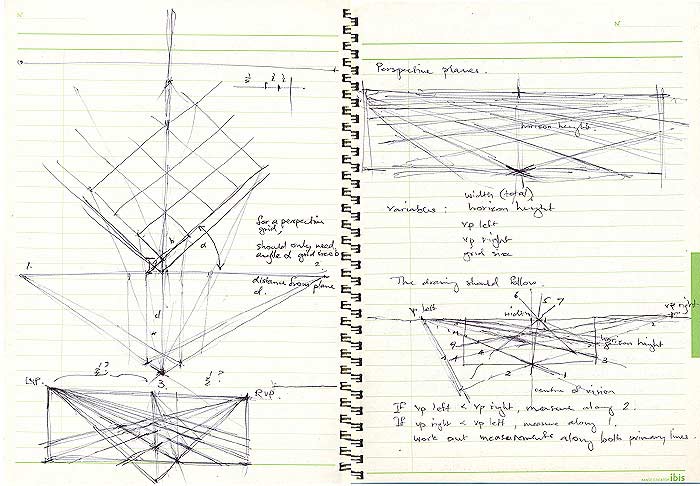
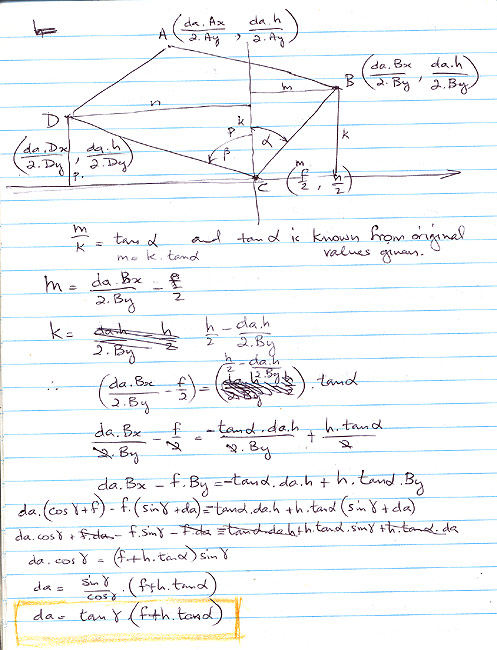
Eventually, I came up with a schema for the procedure:

1. A line at right angles to the horizon is drawn down to the reference point.

2. The length of this line is recorded as the distance of reference point from the horizon (vr).

3. The two vertical reference lines (representing virtual paper edges are then drawn at right angles to the horizon line.

4. The distance between these two vertical lines is recorded as the paper width (pw).

5. The distance is recorded between the left vertical reference line and the vertical line going to the reference point (hr).

6. A virtual bottom paper edge is drawn in, measured evenly below the horizon.

7. The distance from the horizon to the virtual bottom paper edge is recorded (be).

8. where the line going to the right vanishing point from the reference point cuts the right edge of the virtual paper is measured down from the horizon (rx).

9. where the line going to the left vanishing point from the reference point cuts the left edge of the virtual paper is measured down from the horizon (lx).

10. The grid dimension along the line to the left vanishing point is entered (gl)

11. The program then prints out the appropriate dimensions for the lines for the grids along the line to left vanishing point, then for the grid lines along the line to the right vanishing point. The position of the diagonal vanishing point is also given (along the horizon from the left).

I was determined to crack the task. It felt like it should be possible within my understanding of perspective, and geometry.

Showing the measurements that need to be recorded.

Calculating the positions of the left and right Vanishing Points.

Plan of the perspective image construction, with view point, model and picture plane (which is where the perspective projection occurs).

Defining one unit of the model.

Formulae for the points of one unit of the model, with scale factor (s), distance away in the y direction (da), and horizontal offset amount (f).

Looking at the horizontal dimensions of the perspective projection onto the picture plane.

The highlighted boxes show the formulae for the perspective image of the model unit (firstly the horizontal values, then the vertical values).

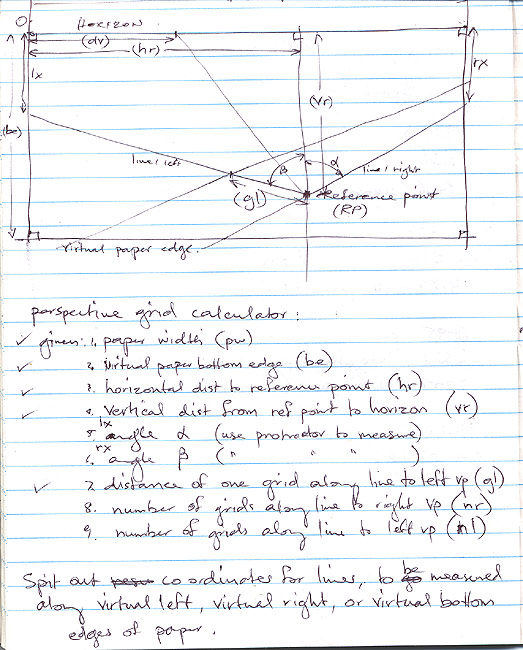
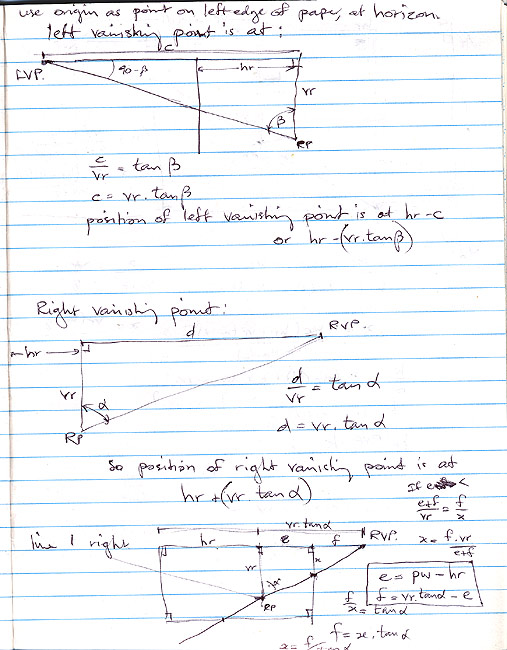
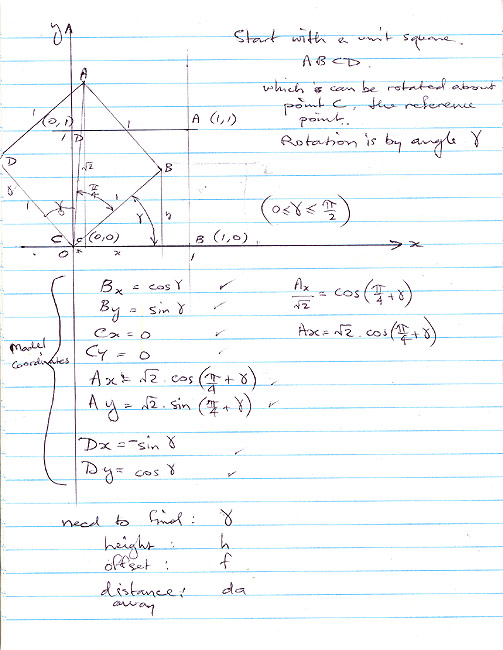
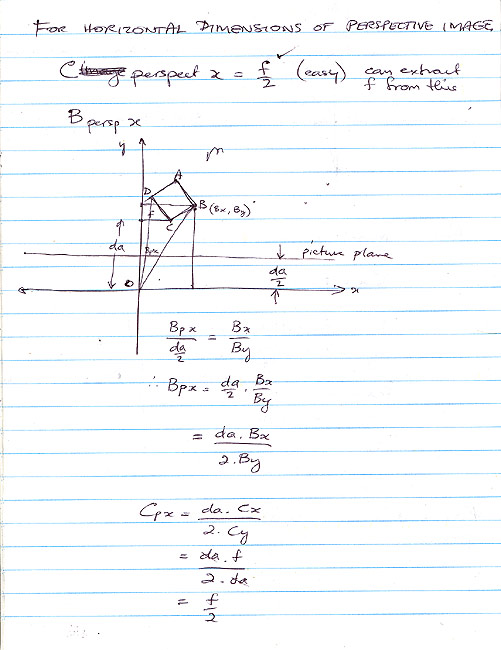
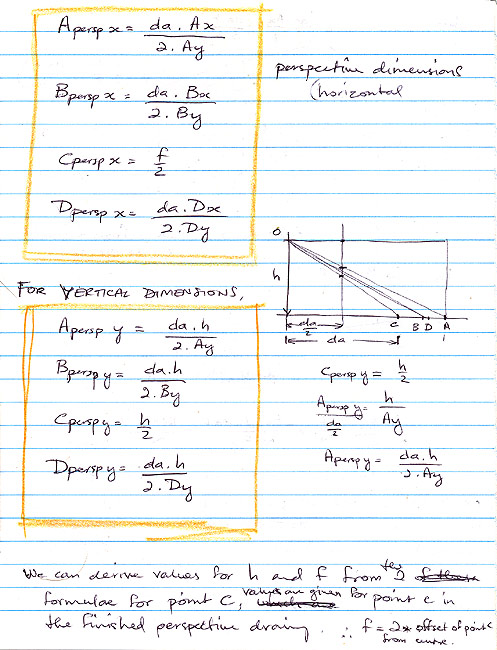
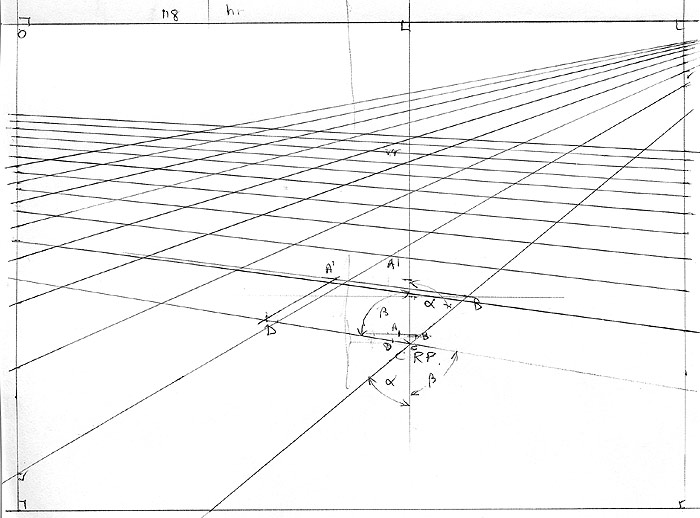
I firstly worked with a spreadsheet for checking some of the formulae I was developing. What I realised was that at some point, I’d have to determine the parameters of a model that could then be used to generate the perspective grid - parameters such as how far away the model is from the viewer, how high the viewer is above the model, the anticlockwise rotation angle of the model of unit squares, the scale factor for the unit squares, and a horizontal offset dimension for the model, from the viewpoint.

To determine the parameters for the model, I’d have to work backwards through the process of generating the perspective grid, from the measurements taken from the drawing.

By using generic mathematical definitions for the points of the model and applying the mathematics required to produce the perspective results, I could then try to solve values for the above parameters. I firstly solved values for how high the viewer was above the model, and the horizontal offset. I was then able to determine the anticlockwise rotation angle of the model, and its distance away from the viewer. This was all very pleasing.

The scale factor proved to be too complex to calculate by solving for a single value within the formulae I had developed.

Instead, I implemented a way of calculating an approximate value, based on trial and error. I firstly started with a scale factor, calculated the resulting points, and then measured the distance between them. If the distance was too small, I increased the scale factor by 1, and recalculated the perspective point positions and the distance between them, etc. If the distance was too big, I then removed 1 from the scale factor, and started a similar series of calculations using 0.1 increments, then 0.01 increments, and finally 0.001 increments. It may sound like it would take a while to do all of these calculations, but today’s computers can do those calculations very quickly indeed.

The highlighted box shows the formula for calculating the distance (da) from the viewpoint to the model.

The highlighted bottom box provides a way of calculating the anticlockwise rotation of the model unit (angle gamma).

Some of the formulae trying to solve for the model scale factor (s) - that I found too complex.

Some of the mapped results, which I find makes an interesting abstract image.

My test image, showing the results of the formulae for the parameters initialised in the finished perspective grid tool.

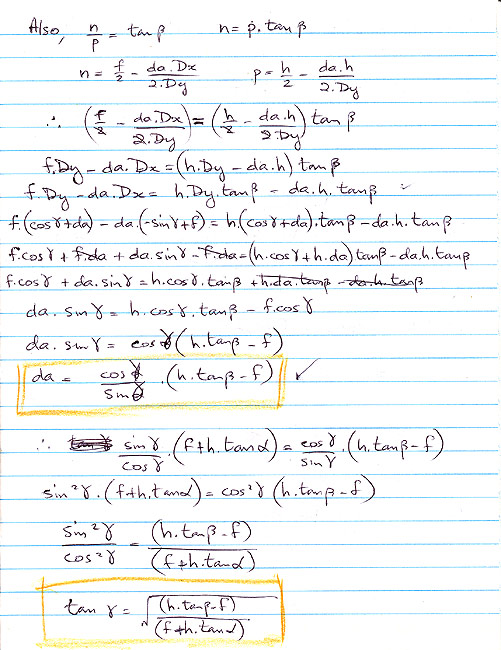
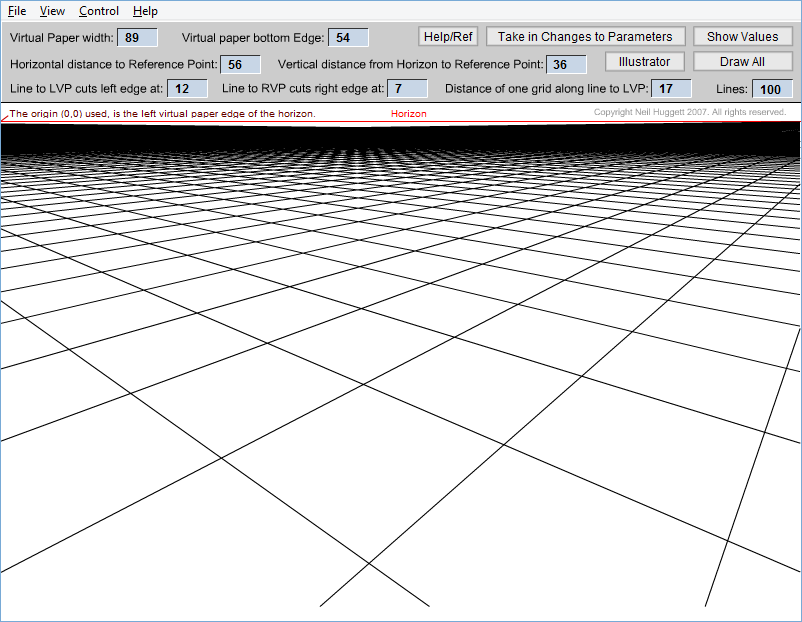
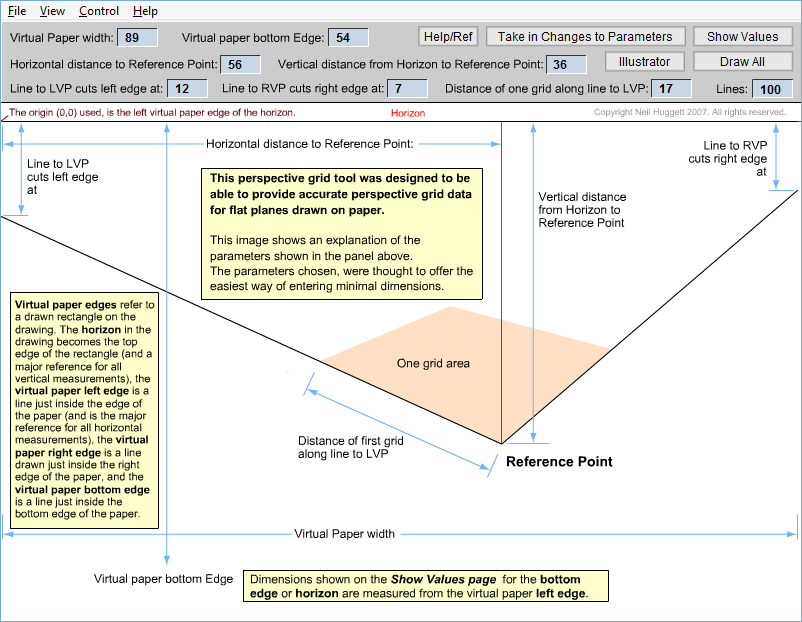
After developing the spreadsheet to get good results, I then decided to create a tool that could show the grid, and provide the measurements required to transfer the grid back onto the drawing the parameters came from. Download the tool from here (right-click on the link and "save as" to your computer for running it from there).